FUSDRG Newsletter
　　　　　南華永續發展研究組簡訊

FUSDRG(Fokuang University Sustainable Development Research Group)

佛光大學南華管理學院永續發展研究組

負責人：陶在樸教授

地址：台灣省嘉義縣大林鎮中坑里32號

網址：http://www.nhmc.edu.tw/html/continue.html(觀迎參觀)

E-MAIL：zaipu@nhmc.edu.tw

電話：00886-5-2720945,2721001

傳真：00886-5-2720234

*(永續發展研究室〝永續論譠〞已正式設置於本研究室網頁中，歡迎大家光臨並發表您們寶貴的意見。)

本期主題： 永續發展工程學

永續發展工程學(Sustainable Engineering)是美國科羅拉多礦業學院Peter Hartley教授提出的一個名稱，其實它並非一般意義下的工程問題，它只是把環境容量看成工程中的材料強度來探討如果超過負荷極限永續性還存在嗎？

Hartley把環境負荷L定義為人口與人均資源消費率的乘積，即

L=C×N

式中C為平均每人的消費，N為人口數，L便是他所謂的人類活動的資源(R)的負荷(或生態負荷或環境負荷)。

所謂資源，應以廣義角度了解，它可能是指一種具體物質，例如石油或煤炭，也可能是指某個物種，甚至它可能是指某個地區的生態系統，有時按討論的興趣所定，如指CO₂排放量不超過某個極限或是水質的純淨度，總之需要記住，當我們吃完一碗飯時，我們不能只說我們消費了稻米，而是我們消費了土地，如果不是為了吃飯田家可以把土地另作用途，地球的表土也不會因為種稻而流失原來的營養。

對於一定的資源R，若以K_L表示環境負荷L所能提供的最大消費量，超過K_L資源R就會出現不可逆的下降或者說失去了可持續性。最重要者，永續工程學所要關注的是人和自然關係的〝使用權〞(Usufrut)約朿，例如，當我們說河流使用權時只是指在一定極限之內你有權使用河水，你不能把何水抽用到使它減少的程度(Worstn, 1985)。你有權使用某種資源，但你無權使用它到任何傷害的程度。這種傷害不僅是指被使用對象的本身，而且是指整個與它有關的生態環境系統，美國蒙大那河水引渡到聖地牙哥是用輸水管抽取黃石河(Yellowstone River)的水而沒有建水壩，就是考慮到水壩淤塞使輸水的永續性破壞。

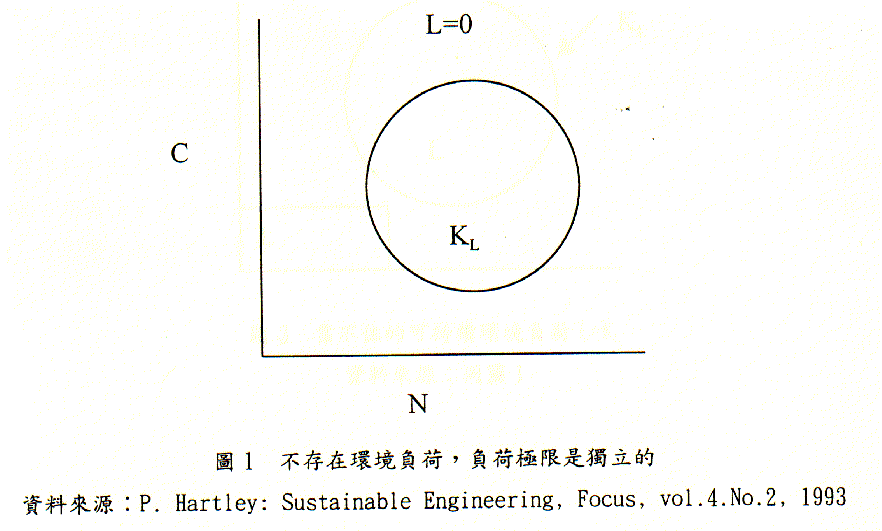
為了深入地說明可持績的等級，我們用一系列的C-N座標圖來討論極限負荷K_L和負荷L的各種關係。圖1中的極限負荷K_L用一個小圓圈來表示，在座標原點附近沒有任何表達，這就是說並無消費(C)也無人口(N)，因此圖1說明的情況是環境負荷L=0時極限負荷K_L與L無關。

　

圖2所要表達的是存在一定的環境負荷L，但是負荷L小於極限負荷K_L，這是一種可持續的環境負荷狀態。圖2座標原點附近，有一個方塊標明L的矩形面積，L等於C×N，因為L＜K_L，這說明這樣的人均資源消費可以無限地延續，只是人口N不能成長。圖中央有兩個圓圈相套，其中一個小圓圈L其面積與矩形面積L相等，大圓圈是K_L。

　

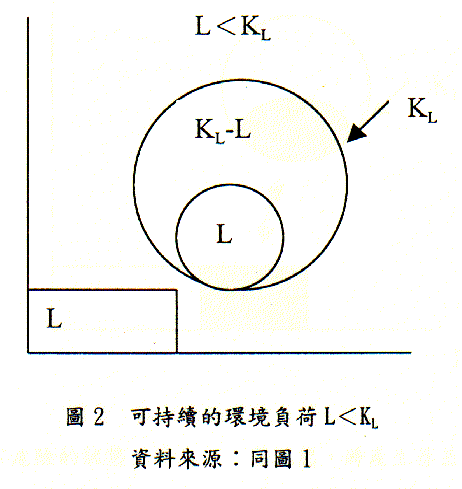
　圖3表示負荷與極限值相等(L=K_L)，這是一種臨界現象(critical phenomenon)，它已經不象圖2留有緩衝空間(K_L-L＞0)，如果L能夠下降則K_L仍可再生(regenerate)，一旦L超過K_L，K_L很可能因不可逆性而再恢復，於是

若L≦K_L，則K_L-L→K_L，而L→0。

我們把圖3這種關係稱為靠不住的可持續負荷L=K_L。

　

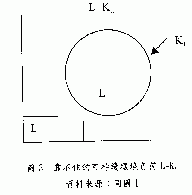
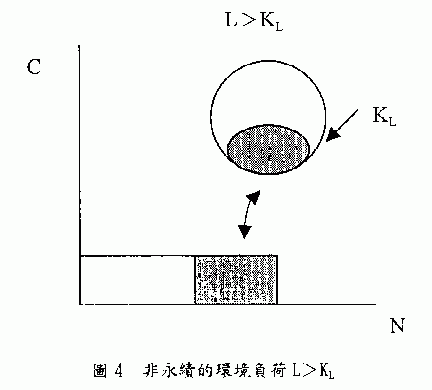
圖4的情況是環境負荷超過極限L＞K_L，在這種超載條件下極限負荷K_L會縮小，圖4中黑色圓圈表示因為超負荷而使K_L永遠失去不可再復生的部分。

你可能想多少就消費多少嗎

人類消費的慾望等級可分成三等，最低者滿足一個有限量以求活下去，這樣的消費記為C_m，農業時代的人大部分如此。隨著工業時代技術的進步和商品的豐富，人類消費慾望爬到最高層，想多少就買多少，這種無限的〝消費所欲消費〞的量記為C_x，工業社會的老牌工業國家大部分如此消費。所謂窮者思變，變甚麼？無非是改變消費慾望，由有限的消費轉變為〝想買甚麼就買甚麼〞的地位轉變，這種消費文化的「窮追富」範式正是人類永續發展的問題所在。理想的消費慾望恰恰在C_m和 C_x兩個極端之間，這種消費一方面需要滿足充足的物質享受水準，另一方面又能滿足世世代代永續發展的要求，把這種消費記為C_r，顯然C_m＜C_r＜C_x。

何以〝消費所欲消費〞的消費方式必需改變？乃因這樣的消費將使環境負荷冪方程成長(圖5)。

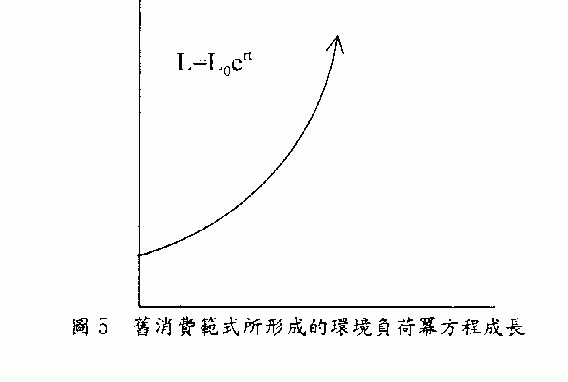
工業宗教對經濟成長率頂禮膜拜，GNP的成長率像汽車的速度錶，它只告訴你跑多快，其慣性在於消費。消費的收入彈性是個常數，於是當經濟指數成長，隨之而得的消費也是指數成長，由消費指數成長最終帶來環境負荷的指數成長，設基始的環境負荷為L₀，指數成長率為r，時間為t，則

L=L₀e^rt

我們經常感到興趣的問題是冪成長時，成倍成長所需要的時間，這個數量增加一倍所需的時間稱為倍增時間(doubling time)，倍增時間與成長常數r的關係如何？

設L₀為某變數L的基始值，經過時間t的指數成長後，成長為基始值的二倍，則

2L₀=L₀e^rt

故 2=e^rt

兩端取對數

ln 2=rt

故倍增時間
ｔ=ln r/r=0.69/r
　

指數成長是一種滾雪球效應而非按比例常數的線性擴張，當成長率很高時系統的狀態變數在很短時間內天文數般的增長，增加一倍的所需的時間越來越少，最後導致系統的崩潰。

生物群數的環境容量

生物群數容量是指一定環境條件下(傳統上是研究一個封閉系統)可持續生存的最大群數(population)，群數的時間動態過程是一個S型曲線(圖6)，群數在第一個階段按冪方程快速成長然後進入第二個緩慢有界的成長階段，最終群數的密度與物種所棲息的面積和環境條件平衡，成長靜止。

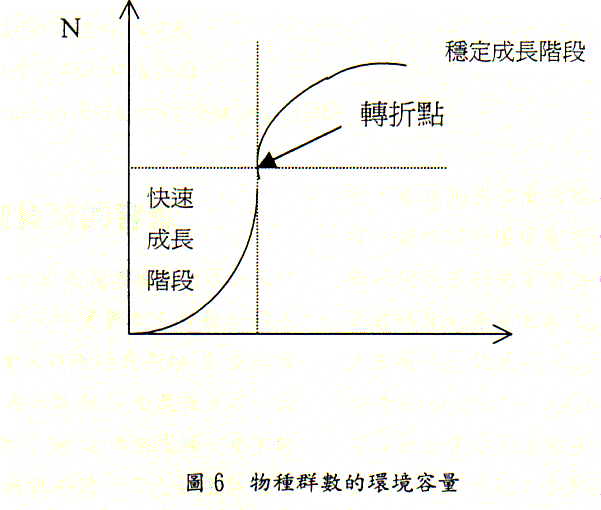
群數的幕方程式如下：

式中 Kn--群數的環境容量

a--環境常數

r--群數成長率

t--時間

e--自然對數之底

由此可以求出群數的變化率

以及常數a

N₀為群數的基始值。

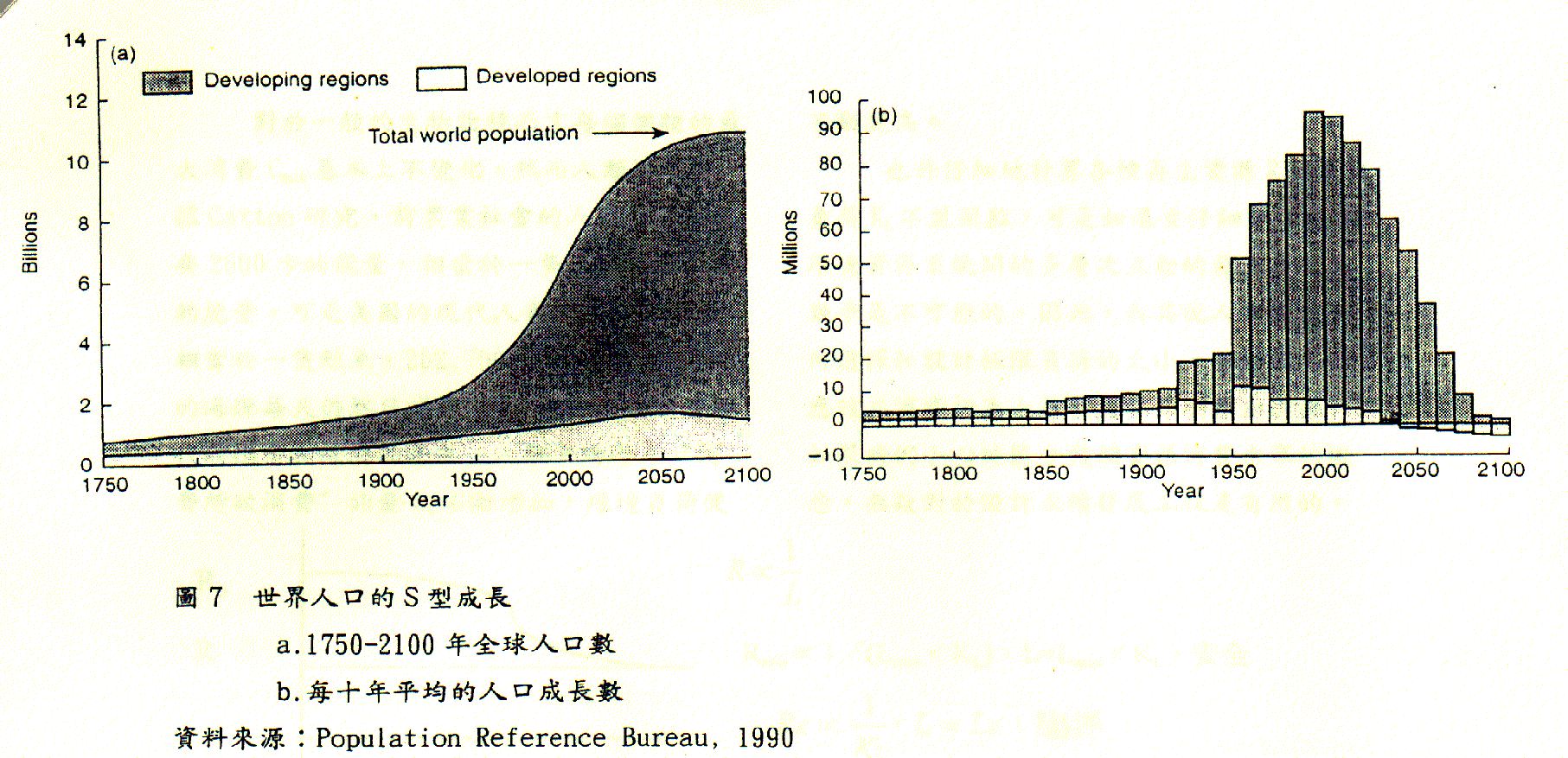
全球人口數的動態成長也未離開S型曲線的基本特徵，1750至1980年為人口指數成長階段，此後進入穩定成長階段，據聯合國人口中心預測2050年以後進入靜止成長，即生死數的平衡階段，估計的最大人口數是110-120億(圖7)

　

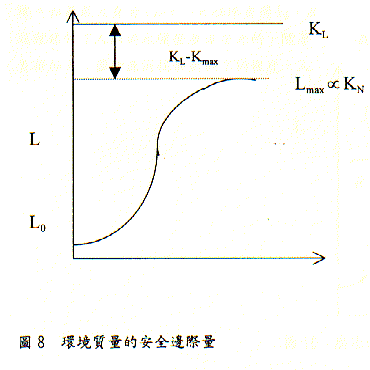
按照Hartley的定義環境負荷等於人口乘人均消費，如果人均消費與人口數無關並維持常數，那麼當人口數的成長按S型曲線時，環境負荷L也必符合S型成長。在一般的討論中也確實把L當S曲線處理，雖不夠準確，但邏輯上也說得通，可是如果討論可持續發展，對L的S曲線參數要有相當多的保留，首先它不同於人口數是一個可觀察的量，誰能夠直接看出環境負荷的大小？即便有一個所謂的環境負荷的極限量K_L，人類活動的環境負荷也不應該超過這個極限，若以允許的最大負荷記為L_max，極限負荷 K_L與最大負荷L_max的差K_L-L_max可稱為環境質量的安全邊際(margin of system quality)(圖8)，可以設想當安全邊際量低於某個數值後整個系統的品質惡化，我們也不能期待惡化後的系統可以立即再修復，這就是環境系統好壞轉化的不可逆性。

對於一般的生物物種而言每個個體的最大消費C_max基本上不變化，然而人類卻不同，據Catton研究，前農業社會的人每天大約需要2600卡的能量，相當於一隻普通海豚所需的能量，可是美國的現代人每天消費的能量相當於一隻鯨魚，202,700卡，而〝現代〞的海豚每天仍然只消費2600卡。人類隨著時代的進步和經濟的發展，人類平均每人〝消費所欲消費〞的量C_x不斷增加，環境負荷便不斷提高。

也許仔細地計算各種再生資源R的最大負荷K_L不並困難，可是如果要仔細評估整個環境資源系統間的多層次互動的最大負荷K_L幾乎是不可能的，因此，與其說人類應該如何選擇和設計極限負荷的大小，不如說人類應該在消費行為上節制與不節制作出選擇。如果我們小心地區分幾個資源消費水準的概念，無疑對於設計永續發展工程是有用的。

　 

整個資源隨著人類活動歷史性的分段減少，假定基始資源為R₀，隨經濟活動(或稱負荷)L的加大而減少，因此R是一條下降的曲線。如果最大負荷Lmax小於極限負荷L_K，在這種條件下人類的永續發展是安全的，隨著負荷加大，因資源消耗加劇的不同程度，人類可能面臨不同的問題，比如使負荷達到極限，資源存量處於臨界狀態，進一步加大負荷，則出現危險。

舊的文化範式和〝消費所欲消費〞的行為將使資源超負荷而崩潰(圖10)

　

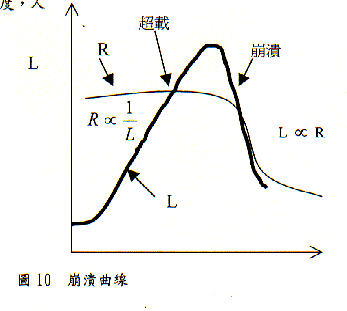
崩潰的發生是非線性的惡性循環，當負荷L冪成長而且不斷突破圖9所示的危險區和臨界區，資源存量迅速下降，一旦負荷衝出了L-R的平衡，環境的允許負荷L與迅速衰減的R同方向下降，R變得越來越小可以承擔的負荷也越來越越小，整個系統最終崩潰。

這些圖示的數值實際上很難朋

撰稿人 陶在樸

參考書目

P. Hartley: Sustainable Engineering, Focus, Vol.4. NO2, 1993

F.Berkes:A system perspective on the interrelations behavior natural, human-made and cultural capital.