二階段式數學迷思概念診斷工具的發展與應用
邱明星
屏科大技術及職業教育研究所
壹、前言
我國九年一貫數學領域之課程綱要於
然而教學者若在教學過程中忽視學生的認知發展和概念學習,勢必使學生以記憶的方式來學習數學知識,其所得的數學知識是死的,容易隨著時間的消逝而遺忘,甚至造成錯誤的理解。因此,教學者在進行數學教學時要能充分瞭解學生每個數學概念的形成,其在教學時應以學生直觀經驗為基礎,經過逐步數學化過程的引導,促使學生建立相關的知識與概念,進而達到數學學習的目標與成效,避免讓學生產生迷思概念。
為使一些科學學科迷思概念的研究獲得更多結果,及能更有效、實際地應用於教學現場上,有些學者提倡發展二階段式(two-tier)概念診斷測驗之必要性(Odom & Barrow,
1995; Treagust,1997)。Treagust(1988,1997)指出,雖然晤談法可深入探究學生的想法,但其具有耗時費力的顧慮,故在一般班級人數多的教室中,教師較易於用以確認學生的迷思概念的方法,還是以紙筆式為多。因此,若能針對某依特定的學科內容,應用既有的研究發現為基礎,設計成紙筆式、選擇題型的二階段式診斷測驗,當更可幫助科學教師了解學生在教學前、後所存的迷思概念,以對症下藥。此外,隨著認知心理學理論的發展及其在科學教育研究上的廣泛應用,現今的教學評量應妥善結合認知科學與心理計量的原理,發展出能夠診斷學生學習錯誤並能測知內在思考機制的認知診斷評量工具,如此方能真正幫助師生達成教與學的成效。迄今,二階段式設計的診斷測驗已陸續發展且應用於數學、物理、化學及生物等學科之學習診斷。
貳、數學迷思概念之探討
迷思概念的研究是來自於建構主義的主張,建構主義以學生為本位的教學,有助於科學教育的傳達。從概念的發展、聯結與分析,導出學習者所具有的最初想法,從而明瞭與發現學習者所具有的迷思概念。因此,迷思概念的診斷與釐清有助於教學的進行,經過概念改變的教學或引導,才能使教學與學習成為有效的活動。就數學知識本身而言,學習新的知識又以舊有的知識經驗作為基礎,依靠學生認知結構進行同化,這過程就是知識的正遷移;相反的,這過程產生的消極作用就是知識的負遷移。當學習的概念混淆不清時,負遷移對數學學習的干擾就可能表現在定理、公式、法則的誤用,及範例的應用錯誤等等情形。
迷思概念產生,可能源自於學生日常生活經驗的自我學習所得;也可能來自於學生對老師機械式敎學的一知半解(呂溪木,1985)。Maurer(1987)也指出在數學學習中,若存有迷思概念,則在演算時,將會產生有系統的錯誤演算規則,此種錯誤的演算規則並非由於學生粗心大意的結果,而是因為不瞭解才產生的。以下是國內外一些相關研究所提出的看法:
一、Booth(1981)在其一篇有關「中學學生的學習方法」(child method in secondary mathematics)的研究中,發現英國的中學生在處理數學問題時,往往不用課堂上老師所教導的方法,反而較常採用自己較有感覺且較有信心的方法。這些較常被學生使用的方法有時效果很好,有時則有其應用上的限制,在學生一知半解的情形下,容易發生產生迷思概念。
二、Schoenfeld(1985)指學生解文字題時,常因為過於依賴句中的關鍵字,因而並未真正的瞭解整個題目的意義。
三、Loftus & Suppes(1972)發現學生解文字題時,表徵「關係命題」(relational propositions:表示變數間的一種量的關係)有困難,例如:「兩年前瑪莉年齡是貝蒂的二倍,瑪莉現年40歲,請問貝蒂現年幾歲?」這一類的問題通常與「語言知識」有關。
四、Ashlock(1990)的研究指出:學生的數學作業不僅是一個分數而已,更要分析;因為導致學生錯誤的原因是錯綜複雜的,使相同的錯誤,也可能是不同的訊息處理過程所導致。
五、秦麗花(1995)引用Rodatz(1979)的研究說明:對教師而言,經由錯誤分析可提供學生學習結果的大量訊息,增進個別化教學成果。相對的,對學生而言,錯誤創造一個新的學習機會,讓學生認識錯誤類型與迷思概念。因此,探討學生的錯誤類型和迷思概念是有必要的。
六、楊弢亮(1992)在他所著的「中學數學教學法通論」中,將學生產生迷思概念的原因,歸納為下列幾種:(一)概念混淆;(二)定義不明確;(三)定理理解不清楚;(四)
條件不注意;(五)邏輯錯誤;(六)法則不會;(七)公式記錯;(八)計算錯誤。
七、張景媛(1994)由研究結果指出:蒐集數學解題時學生可能產生的迷思概念,並加以分類,至少有下列幾點助益:
(一)可讓數學教師瞭解學生有可能犯錯的概念,使其教學時能注意學生的學習困難,而改善其教學方式。
(二)提供數學教師在評量學生時命題的參考,教師也可針對學生易犯的錯誤概念命題,以偵測學生學習困難之所在。
(三)提供數學教師在進行個別輔導教學時的參考。
(四)可作為數學教材編輯者的參考。
綜合以上所述,若依皮亞傑的認知發展來看,國小數學著重於具體操作的教學,而國中數學卻以形式運思期的抽象思考和邏輯推理為主,在教材和教法上都有明顯的不同。而對剛從國民小學升上國民中學一年級的學生而言,以其熟悉的數學學習方式改變成不熟悉的思考方式,這種思考的過程當中又會引發許多的迷思概念。因此,在國民中學階段的教師應於教學時,以多發問並鼓勵學生發問的方式,發現學生的回答中可能有的錯誤概念,再依其情形,設計適當且適合學生的教學方案,協助學生思考自己所犯的錯誤,幫助他們建立正確的概念。
參、二階段式數學迷思概念診斷測驗的發展與應用
根據Nichols(1994)的建議,認知診斷測驗的設計應包含建構實質理論(substantive
theory construction)、選擇設計(design selection)、執行測驗(test administration)、反應評分(response scoring)與修正設計(design revision)等階段。Treagust(1988, 1997)與Odem 和Barrow(1995)亦提出發展二階段式診斷測驗的具體程序,二階段式數學迷思概念診斷工具發展之流程,如圖1所示。
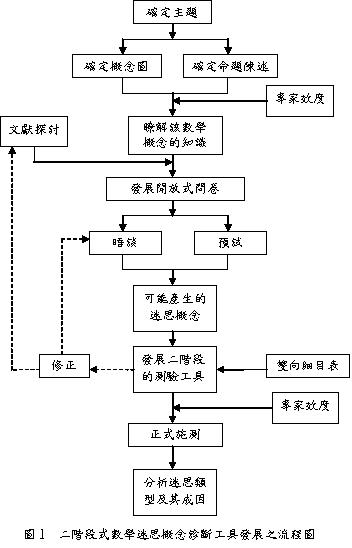
![]() 以下就數學迷思概念為例,說明二階段式診斷工具發展的流程,其一般共分為三個階段,十個步驟,分述如下:
以下就數學迷思概念為例,說明二階段式診斷工具發展的流程,其一般共分為三個階段,十個步驟,分述如下:
一、界定內容(包含四個步驟)
(一)分析所界定之數學學習單元之內容,確認命題知識(propositionknowledge)的敘述。
(二)發展數學學習單元內容所含概念之概念圖。
(三)檢視概念圖所含的概念與命題知識的敘述均涵蓋相同的內容。
(四)效化內容;請專家學者和資深教師效化與修正命題知識的敘述和概念圖。
二、收集關於學生迷思概念的訊息(包含三個步驟)
(五)回顧相關的研究文獻,以建立發展選擇題的訊息基礎。
(六)執行非結構化的學生或教師晤談,以求對所欲探究學生的迷思概念有更廣泛的觀點。
(七)發展帶有自由回答項目之選擇題式的試題:每題題後均有一處可讓受試學生填寫為何選擇某一選項的原因,以便由各題之自由回答的部分,發現更多學生的想法。
三、發展診斷工具(包含四個步驟)
(八)發展二階段式的診斷工具:每個題目的第一階段是選擇題,主要在評測學科單元的內容知識。第二階段的選擇題每題均包含幾個可能選答某一選項的原因。這些原因包括正確的答案、經確認的迷思概念或純粹是錯誤的答案。評分時唯有二段都答對才算正確。
(九)設計一個雙向細目表(specification grid),用以確保診斷工具能均勻、完全地涵蓋學科單元內容所含之命題知識敘述和概念圖中的所有概念。
(十)不斷的改良;透過持續地回顧迷思概念之研究文獻、晤談學生、老師和蒐集相關的試題等方式,針對診斷測驗的試題不斷地加以改良或修正,以使該測驗能迎合需要。
以上發展歷程主要參考Treagust(1988)所提出的建議程序,稍作調整而成。二階段式數學迷思概念診斷測驗可作為成就測驗及探究迷思概念的工具,不少國中學生雖在傳統教學中獲得記憶性的知識,而能在第一階段正確作答,卻在第二階段中顯示出對數學概念未真正瞭解。教學者可在一個特定主題單元教學的開始或結束時使用這種評量工具,若將其運用在數理、自然科學等領域上,教師將能夠更清楚、且有效率地瞭解學生的認知概念與架構,包括學生所持有的迷思概念。
肆、結語
在數學領域教學、學習的實務與研究上,認知心理學的觀點已被廣泛地應用。因此,評量測驗工具的發展自然也應符合認知心理學的理念,數學領域的教師不能只滿足於學生在傳統測驗題評量的高分,而忽略其真正的想法。二階段式數學迷思概念診斷測驗因具備實施容易、省時、可大量使用等優點,又可幫助數學領域教師從診斷測驗的結果迅速得知學生數學概念學習的情況,作為日後補救教學的參考。而學生亦可由診斷測驗的結果,清楚自己在數學概念學習的困難或迷思之處,有助於日後的加強學習。
雖然二階段式數學迷思概念診斷測驗的發展較費時,但因為在試題上精心的設計與安排,讓教學者、學習者與研究者能從評量測驗的結果中獲得更多、更有幫助的訊息,如此,無論就教、學與研究而言,方能有更實質的意義與價值。另外,二階段式概念診斷測驗工具也可設置在電腦網站中,提供學生自我評量的目的,而迷思概念的類型也可利用資料庫予以建立與統整。因此,二階段式數學迷思概念診斷測驗工具的發展與應用,將是日後促進數學領域教學與學習成效的一種利器。
參考文獻
呂溪木(1985)。從國際科展看我國今後科學教育發展的方向。科學教育月刊,64,13-19。
秦麗花(1995)。國小數學學障兒童數學解題錯誤類型之分析。特殊教育季刊。55,33-38。
教育部(2000)。國民中小學九年一貫課程綱要數學學習領域。台北:教育部。
張景媛(1994)。數學文字題錯誤概念分析及學生建構數學概念的研究。國立台灣師範大學教育心理與輔導學系教育心理學報,27,175-200。
楊弢亮(1992)。中學數學教學法通論。台北:九章出版社。
Ashlock, R.B.(1990).Error
patterns in computation: A
semi-programmed approach(5thed).Columbus,
Booth, R.L.(1988).Children’s difficulties in beginning algebra.
In A.E. Coxford and A.P. Shulte. The ideas of algebra, K-12. 1988 Yearbook.
The National Council of Teachers of Mathematic Virginia,
Loftus, E.F. & Suppes,
p.(1972).Structural Variables that Determine
problem-solving Difficulty in computer Assisted Instruction. Journal of Educational Psychology,63, 531-542.
Maurer, S.B.(1987).
New Knowledge about Errors and new Biews about
Learners: What They Mean to Educations and More Educators Would Like to Know.
In A.H. Schoenfeld(Ed.), Cognitive
Science and mathematics Education, 165-187.
Nichols, P. D. (1994). A
framework for developing cognitively diagnostic assessments. Review of Educational Research, 64(4),
575-603.
Odom, A. L., &
Barrow, L. H. (1995).
Development and application of a two-tier diagnostic test measuring college
biology students’ understanding of diffusion and osmosis
after a course of instruction. JRST,
32(1), 45-61.
Shoenfeld, A.H.(1985). Mathematical Problem
Solving.
Treagust, D. F. (1988). Development and use of diagnostic tests to
evaluate students’ misconceptions in science. International Journal of Science Education,
10 (2), 159-169.
Treagust, D. F. (1997). Diagnostic
assessment of students’ science knowledge. Paper presented at the 1997 International
workshop on student’s
concept development, understanding diagnosis and teaching. Feb.
17-20,